前言
之前学校开的选修课《数据挖掘》,布置的两道算法题,时间有限完成其中一道:用Apriori算法求特定支持度的频繁项集。
算法本身不难,java萌新我却花费了一天的时间,特此记录。
算法描述
我们目的是求出项数为K的频繁项集即L(K)。
Apriori算法的核心步骤是:
- L(K-1)通过自连接求出项数为K的候选项集合C(K)
- 通过对C(K)进行一系列处理(剪枝 + 支持度判断) 得到L(K)集合
在说明下面更多内容之前,先对一部分概念进行说明:
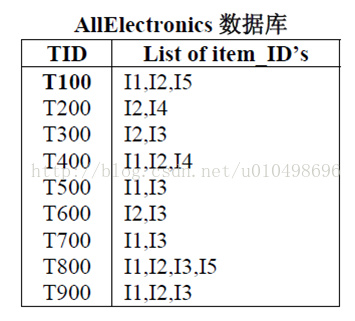
- 事务:如第一张图中,每一行就是一个事务,如
T100 I1,I2,I5。其中T100是事务编号,这个随便命名,只要保证唯一即可。后面的I1 I2 I5是该事务中的项 - 数据集:如图一,整个表就是数据集,就是所有的事务的集合。即D = {T100,T200…}
- 项集:包含若干个项(如I1 、I2这样的项)的集合。可以看出项集和事务似乎有点项。但是项集更随意一点,任意几个项都能组成一个项集。但是事务是人为规定好的。
- 可信度:项集在数据集中出现的重复次数。项集不一定需要在事务中连续出现。如{I1,I2,I5}项集在数据集中出现的次数为2次,分别是第一个和倒数第二个事务。
接下来,详细分析算法中的两个步骤:
1. 自连接:
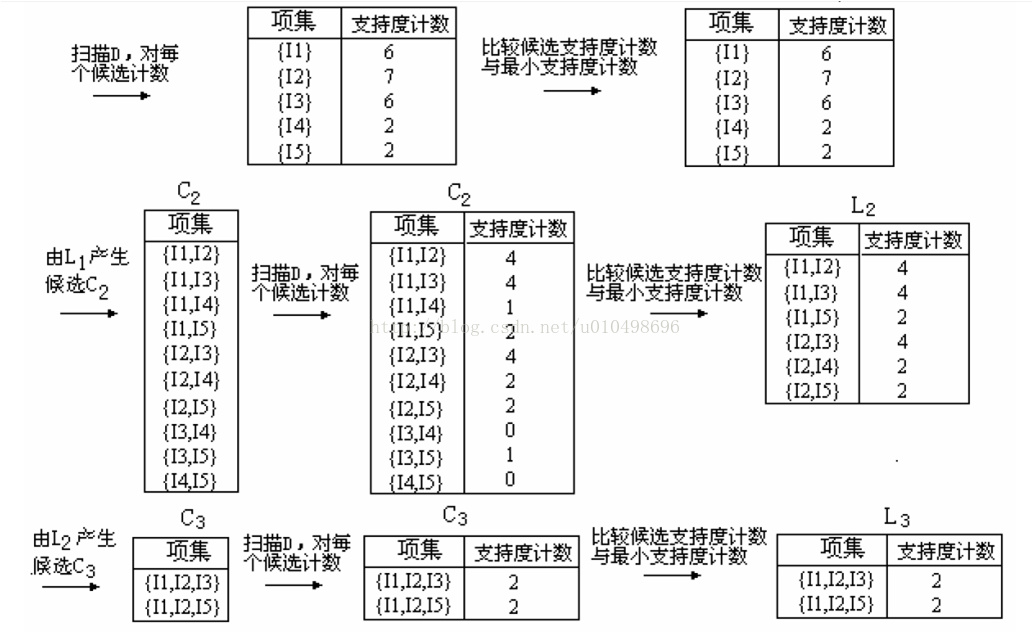
怎么个连接法呢?以图二中的L2频繁集的集合为例:
| 项集 | 支持度 |
|---|---|
| {I1,I2} | 4 |
| {I1,I3} | 4 |
| {I1,I5} | 2 |
| {I2,I3} | 4 |
| {I2,I4} | 2 |
| {I2,I5} | 2 |
判断两个项集是否可以自连接要看两个项集的K-1项是否完全相同。如果满足条件,连接后的项集 = 第一个项集 + 第二个项集的最后一个元素。
比如{I1 I2}与{I1 I3}满足自连接条件,连接后的项集为{I1 I2 I3}。
2. 剪枝:
剪枝是这个算法的核心,如果不进行这个步骤的话,也能得出正确结果,但是时间就会大大增加了。
剪枝的核心是若某个集合存在一个非空子集不是频繁项集,则该集合不是频繁项集。
我们通过自连接组成新的K项的候选项集后,需要通过剪枝判断是否满足条件。
即找出该候选项集的含有(K-1)项的子集,并分别判断每个子集是否存在于K-1项频繁项集里。只要有一个不存在,那么该K项候选项集也不可能是频繁项集。
这里我们只需要找含有K-1项的子集,而不用找所有的子集,因为这个算法是从下不断递归上来的,含有更少项的子集肯定是在频繁子集里的。
问题关键是怎么寻找某个K项集的K-1项子集呢?
很简单,依次把K项集中的每个元素去掉一个就可以了。
完成了这两步骤,就完成了这个算法了核心步骤。
3. 对精简后候选集统计每一个项集的支持度
4. 根据最小支持度将候选项集转换为K项频繁项集合
可以看出,如果不剪枝的话,第三步的工作量是非常大的。剪枝过后,候选集的体积大大减小了。
但是获取含有一项的频繁项集因为没有候选项集,就需要特殊处理。
这个很简单,就是统计数据集中的每一项的支持度,并和最小支持度进行比较,得到含有一项的频繁项集。
代码分析
github项目地址:https://github.com/ihewro/Apriori
import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.*;
/**
* @author hw
* 算法名称:数据挖掘:Apriori算法求特性支持度下的所有的频繁集
* 算法原理:
*
* 0. 获取C1的时候,因为没有L(0)频繁集,所以单独处理一个函数
* 1. 已经频繁集L(k-1),{}自连接+剪枝}求出精简后的候选集C(k)
* 2. 根据精简后的候选集C(k)根据求出频繁集L(k)
*
* 数据结构:
* 1. 使用List<String> 存储整个数据库的数据,string代表每一行的数据
* 2. 使用HashMap<String,Integer> 存储项集以及项集的重复次数,便于查找。是{项集}的集合。
* 3. 每个项集用String类型存储。项集中的每一项使用String.split(" ")方法变成数据,以便取用项集中的每一项
*
* 给定的数据格式:
* 1. 每个数据以空格隔开
* 2. 每一行代表一个事务T,事务编号就是行号
*
* 示例数据:
* 1. {11,12,13}是一个频繁项集,是属于HashMap<String,Integer>中的一个元素,数据类型为String.
* 2. Set<String> = HashMap.keySet(); 用来存储HashMap的所有key的值,也就是存储所有的项集(不包括项集的重复次数)
*
* 相关概念:
* 1. 支持度百分比
* 2. 支持度
* 3. 事务
* 4. 候选项集
* 5. 频繁项集
*/
public class Main {
private static double SUPPORT_PERCENT = 0.01;
private static List<String> data2DList = new ArrayList<>();
public static void main(String[] args) {
System.out.println("===================Apriori算法主程序界面====================");
//0. 输入数据
/*Scanner in=new Scanner(System.in);
SUPPORT_PERCENT = in.nextDouble();*/
//1. 导入数据
importData();
//2. 进行算法处理
apriori();
}
/**
* Apriori算法主程序,需要递归处理
*
* @return
*/
public static void apriori(){
//扫描整个数据库D,对每一项进行计数,获得一项的{候选项集合}
Map<String, Integer> stepFrequentSetMap = new HashMap<>();
System.out.println("\n=====================第" + 1 + "次扫描的频繁项集列表======================" + "\n");
stepFrequentSetMap.putAll(getFrequentSets(findCandidateOneSets()));
Set<String> stringSet = stepFrequentSetMap.keySet();
for (String string: stringSet){
System.out.println("频繁集:" + string + "支持度:" + stepFrequentSetMap.get(string));
}
System.out.println("\n频繁项集的个数:" + stringSet.size());
int i = 1;
//当生成的频繁项集为空的时候,退出循环
while(stepFrequentSetMap != null && stepFrequentSetMap.size()>0){
i++;
//打印当前的频繁项集的信息
System.out.println("\n=====================第" + i + "次扫描的频繁项集列表======================" + "\n");
stepFrequentSetMap = getFrequentSets(getMinCandidate(stepFrequentSetMap));
if (stepFrequentSetMap != null){
stringSet = stepFrequentSetMap.keySet();
for (String string: stringSet){
System.out.println("频繁集:" + string + "支持度:" + stepFrequentSetMap.get(string));
}
System.out.println("\n频繁项集的个数:" + stringSet.size());
}
}
}
/**
* 导入数据
*
* @return 集合和集合,即二维集合
*/
private static void importData(){
File file = new File("retail.dat");
try {
//文件存在且为文件类型执行接下来的操作
if (file.isFile() && file.exists()){
InputStreamReader reader = new InputStreamReader(new FileInputStream(file),
"UTF-8");
BufferedReader bufferedReader = new BufferedReader(reader);
String lineTxt;
while ((lineTxt = bufferedReader.readLine()) != null){//读取文件中的一行
data2DList.add(lineTxt);
}
reader.close();
}else {
System.err.println("找不到指定文件!");
}
}catch (Exception e){
System.err.println("读取文件内容出错!");
e.printStackTrace();
}
}
/**
* 寻找1项的候选集C1(起始化特殊的处理)
*
* @return 返回map集合,这个集合是每一项以及对应的重复次数:key->value
*
* key:每一个候选项/频繁项
* value:相应候选项/频繁项的重复次数
*/
private static HashMap<String, Integer> findCandidateOneSets()
{
HashMap<String, Integer> resultSetMap = new HashMap<>();
for(String dataList :data2DList)
{
String[] dataString = dataList.split(" ");
//查询map集合中是否有该元素,如果没有,加入该元素,否则给该元素对于的value(重复次数)+1
for (String string :dataString){
string += " ";
if (resultSetMap.get(string) == null){
resultSetMap.put(string,1);
}else {
resultSetMap.put(string,resultSetMap.get(string) + 1);
}
}
}
return resultSetMap;
}
/**
* 从L(k-1)频繁集合中得到精简的C(k)候选集
*
* 1. {连接 + 剪枝} = {精简后的候选集C(k)}
* 是对L(k-1)频繁集的每一个集合,进行[边连接成候选集,边剪枝]而不是先全部生成了{候选集},然后再进行一次大循环,进行剪枝,这样会增加时间复杂度
*
* 先验原则:若某个集合存在一个非空子集不是频繁项集,则该集合不是频繁项集
*
* 1. 根据先验原则压缩候选集大小后得到精简的候选集集合
* 2. 对精简过的候选项集进行累加计数
*
* @param frequentMapSet
* @return 返回C(k)候选集合
*/
private static Map<String, Integer> getMinCandidate(Map<String, Integer> frequentMapSet){
//需要返回的精简过后的候选项集
Map<String,Integer> minCandidateMapSet = new HashMap<>();
//导入频繁项集的KEY
Set<String> frequentSet = frequentMapSet.keySet();
/**
* 1. {自连接过程:产生候选项集}
*
* 对于每一个项集,拆开成项的数组。将该项集的每一项与其他项集的每一项比较,
* 如果有不重复的项,就将该项与原项集链接起来,组成K项的候选项项集。
*/
for (String frequentItemList1: frequentSet){
for (String frequentItemList2: frequentSet){
String[] itemArray1 = frequentItemList1.split(" ");
String[] itemArray2 = frequentItemList2.split(" ");
//自连接生成的候选项集
String linkString = "";
boolean flag = true;//是否可以连接
/**
* 判断是否可以自连接的条件:
* 1. 前K-1项必须相同
* 2. itemArray1的最后一项必须小于第二个项集的最后一项
* 自连接过程:
* 将第一个项集与第二个项集的最后一项连接起来
*/
for (int i =0;i<itemArray1.length -1 ;i++){
if (!itemArray1[i].equals(itemArray2[i])){
flag = false;
break;
}
}
if (flag && itemArray1[itemArray1.length - 1].compareTo(itemArray2[itemArray1.length -1]) < 0){
linkString = frequentItemList1 + itemArray2[itemArray2.length - 1] + " ";
}
/**
* 2. {剪枝过程,也就是先验规则的使用}
*
* 找出该候选集的所有子集,并判断每个子集是否属于频繁子集
*/
boolean hasInfrequentSubSet = false;// 是否有非频繁子项集,默认无
if (linkString != ""){//自连接成功
//System.out.println(linkString);
//候选项集的所有项的数组
String[] itemArray = linkString.split(" ");
//*重点:找出该候选集的所有子集,实际操作的时候只需要找出比候选集少一项的子集集合
//*重点:因为这都是不断的递归上来的,项数更小的项集肯定是频繁项集
for (int i = 0; i <itemArray.length; i++){
String subString = "";
for (int j = 0;j<itemArray.length; j++){
if (j!=i){
subString += itemArray[j] + " ";
}
}
if (frequentMapSet.get(subString) == null){
hasInfrequentSubSet = true;
break;
}
}
}else{
hasInfrequentSubSet = true;//这里并不是代表存在非频繁子集,只是表示没有自连接成功,没有找到候选集
}
//自连接成功,加入到候选集集合中
if (!hasInfrequentSubSet){
minCandidateMapSet.put(linkString,0);
}
}
}
/**
* 3. {对生成的候选集进行统计支持度}
*/
Set<String> minCandidateSet = minCandidateMapSet.keySet();
// 将每一行的候选项集,由String数据变成字符串数组。
// 将每一行的事务,由String转换成List<String>
for (String itemList: minCandidateSet){
String[] strings = itemList.split(" ");
int num = 0;
for (String data:data2DList){
List<String>dataList = Arrays.asList(data.split(" "));
Boolean flag = true;
//如果候选项集中有一项在当前事务中找不到,支持度则不会增加
for (int i =0;i < strings.length;i++){
if (!dataList.contains(strings[i])){
flag = false;
break;
}
}
if (flag){
minCandidateMapSet.put(itemList,minCandidateMapSet.get(itemList) + 1);
}
}
}
return minCandidateMapSet;
}
/**
* 从精简后的C(k)候选集中得到L(k)频繁集合
*
* {统计精简后的候选集C(k)的重复次数} = {最后得到L(k)频繁集}
*
* 1. 对精简过的候选集进行判断(之前已经做好了计数工作),不满足支持度的进行排除
*
* @param minCandidateMapSet
* @return
*/
private static Map<String, Integer> getFrequentSets(Map<String, Integer> minCandidateMapSet){
if (minCandidateMapSet == null){
//精简后的候选集为空,表示当前项数的候选集不存在,此时需要结束该算法了
System.err.println("候选项集为空");
return null;
}else{
Map<String,Integer> frequentMapSet = new HashMap<>();//需要返回的频繁项集
Set<String> minCandidateSet = minCandidateMapSet.keySet();//获取候选项集的KEY,也就是所有的项集的具体数据
Double SUPPORT = (data2DList.size() * SUPPORT_PERCENT);//最小支持度
//Double SUPPORT = 5.0;
System.out.println("最小支持度为:" + SUPPORT + " 候选项集的大小为:" + minCandidateMapSet.size() + "\n");
for (String itemListString: minCandidateSet){
//如果该项集的重复次数大于或者等于最小支持度,就把该项加入到频繁项即中
if (minCandidateMapSet.get(itemListString) >= SUPPORT){
frequentMapSet.put(itemListString,minCandidateMapSet.get(itemListString));
}
}
if (frequentMapSet.size() == 0){
//计算得到的频繁项集为空,表示此时循环应该结束了
return null;
}else{
return frequentMapSet;
}
}
}
}
14 条评论
剪枝的时候要判断前k-1项相同 但是先完成一项频繁集的搜索之后 每个key值还都只有一个元素啊 长度是1 那个213行的循环根本就进不去 这是怎么操作的呢? 我哪里漏看了么?
每个key 是一个项集的字符串,包含多个事务的,可以根据空格分割开来的
好像当数据里一行中出现两个相同数据时,会出现问题
好久没看这个算法了,可以根据注释看看能不能改一下
请问,这个元数据文件是什么文件呢?
retail.dat --原始文件
test.dat -- 截取部分数据的文件,方便更快测试
这两个文件
博主,那个判断203行前 k-1 项必须相等是不是少了个 "!"
确实应该加个
!,你可以修改后再运行下测试数据算法很清晰,有个问题
在判断是否可以自连接的条件这里
itemArray1的最后一项必须小于第二个项集的最后一项
为什么还有个这个条件
太感谢了 大作业就是你了
很早以前写的了,现在印象不是很深。我的理解是避免自连接生成重复的候选项:
比如
{I1,I2}
{I1,I3}
条件I2 < I3 ,可以连接{I1,I2.I3}
{I1,I3}
{I1,I2}
条件不符合I3<I2,所以不会再次连接{I1,I3,I2}
OωO 谢谢
请问你的测试用例能不能拿出来看看
直接可以看下github项目里:https://github.com/ihewro/Apriori
里面有:retail.dat 是原始测试数据(老师给的),这个大概需要80s才能跑完
test.dat 是自己测试用的,是从原始测试数据中截取的一段,跑这个很快的